Maclaurinシリーズと特定の関数の分解

より高い数学を勉強することは、与えられた系列の収束の区間に属するべき級数の和は、連続的かつ無限に何度も異なる差別化関数であることを意味する。疑問が生じます：与えられた任意の関数f（x）がべき級数の和であることを主張することは可能ですか？つまり、f番目のf（x）はどのような条件の下でべき級数で表すことができますか？このような問題の重要性は、f（x）を、べき級数のいくつかの第1項の和、すなわち多項式で近似的に置き換えることが可能であることである。そのような関数を多少単純な式（多項式）で置き換えることは、数学的分析のある問題、すなわち積分を解くこと、微分方程式を計算することなどの問題を解決するのにも便利である。

最後のものを含めて（n + 1）次までの導関数を（α（α））の近傍で計算することができるいくつかのf関数f（x）について、 - R; x₀+ R）には、次の式が有効です。

この公式は有名な科学者ブルック・テイラーの名前を冠しています。以前のものから得られたシリーズはMaclaurinシリーズと呼ばれます：

Maclaurinシリーズに分解することを可能にするルール：

第1、第2、第3の順序の導関数を決定する。
x = 0での導関数が等しいものを計算します。
与えられた関数のMaclaurinシリーズを記録し、その収束の間隔を決定する。
間隔（-R; R）を決定します。ここで、Maclaurin式の残り

R_n（x）→0をn - >無限大とする。それが存在する場合、その中の関数f（x）はMaclaurin系列の和と一致しなければならない。

私たちは現在、Maclaurinシリーズを個々の機能について検討しています。

したがって、第1は、f（x）= e^x。もちろん、その特異性の観点から、そのような関数は非常に異なる次数の導関数を持ち、f^（k）（x）= e^xここで、kはすべての自然数に等しい。 x = 0に置き換えます。我々はf^（k）（0）= e⁰= 1、k = 1,2 ...前述から分かるように、系列e^x次のようになります：

関数f（x）= sin xに対するマクローリン系列。直ちに、すべての未知数に対するf-Iaがf^"（x）= cos x = sin（x + n / 2）、f^""（x）= -sin x = sin（x + 2 * n / 2）...、f^（k）（x）= sin（x + k * n / 2）ここで、kは任意の自然数である。すなわち、簡単な計算を行った結果、f（x）= sin xの系列は次のような形になると結論づけることができます。

3.ここで、f-yy f（x）= cos xを考慮しようとします。すべての未知数に対して、任意の次数の導関数を持ち、| f^（k）（x）|再び、ある計算を行った後、f（x）= cos xの系列が次のようになることがわかります：

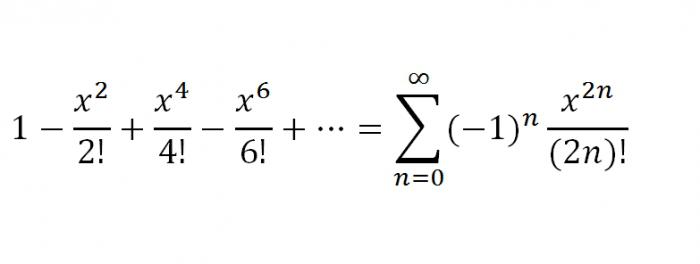
だから、私たちは、Maclaurinシリーズに分解できますが、いくつかの機能のためにTaylorシリーズで補完されています。今度はそれらをリストアップします。また、TaylorとMaclaurinシリーズは高次数学のシリーズを解くためのワークショップの重要な部分であることにも注目しています。だから、テイラーはランクされる。

1.最初は関数f（x）= ln（1 + x）の系列となる。前の例と同様に、与えられたf（x）= ln（1 + x）に対して、Maclaurinシリーズの一般形式を使って系列を追加することができます。しかし、この機能では、Maclaurinシリーズをもっと簡単に入手することができます。ある幾何学的系列を積分すると、そのような標本のf（x）= ln（1 + x）の系列が得られる。

2.そして最後の記事は、f（x）= arctan xの系列となります。区間[-1; 1]に属するxについて、分解は有効である：

それだけです。この記事では、特に経済と技術の大学で、数学で最も広く使われているTaylorとMaclaurinシリーズを調べました。